Additional Exercise Solutions

fpp3 1.8, Ex 1

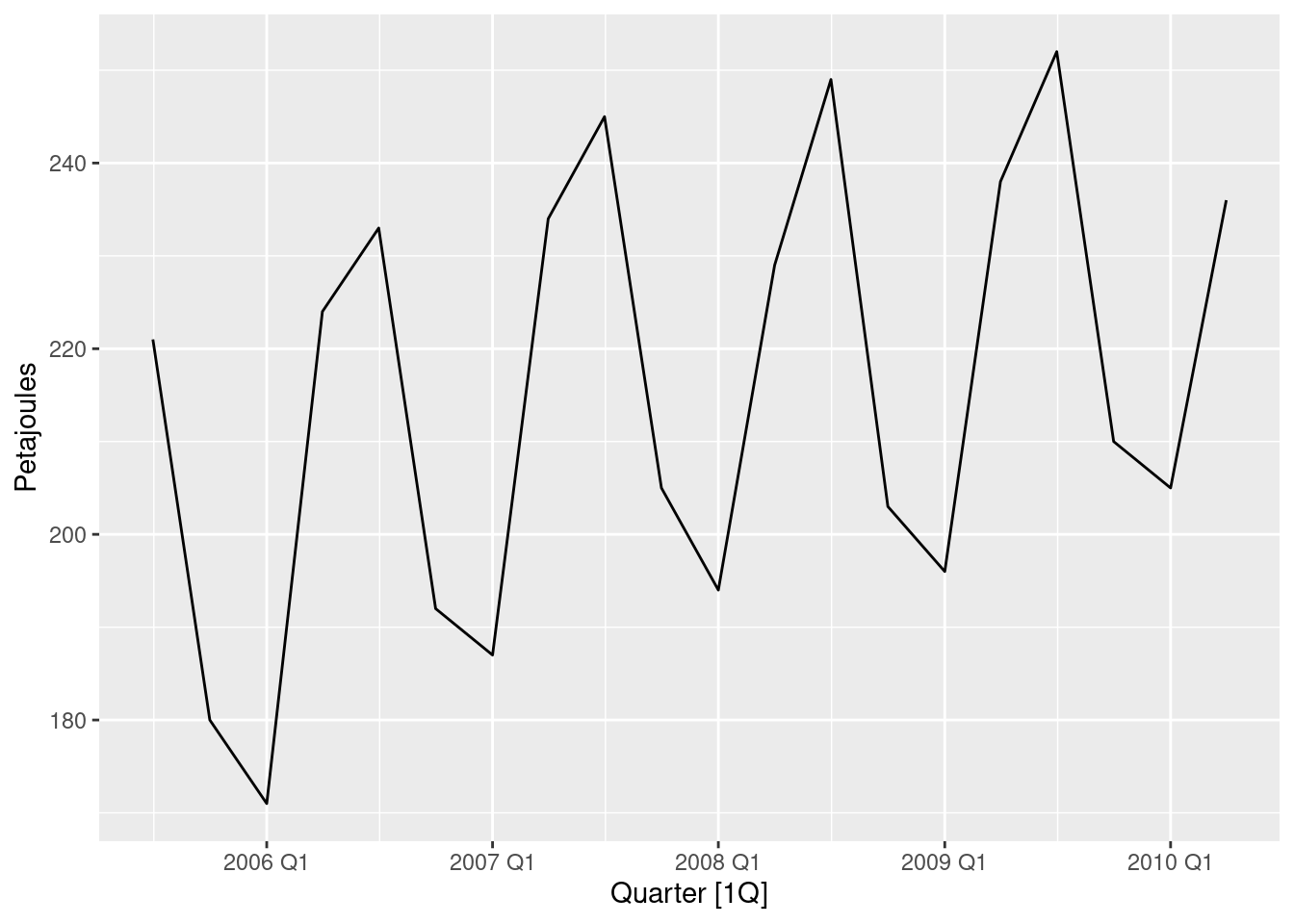
For cases 3 and 4 in Section 1.5, list the possible predictor variables that might be useful, assuming that the relevant data are available.

Case 3: the following predictor variables might be useful, assuming that the relevant data are available:

  • Model and make of the vehicle
  • Odometer reading
  • Conditions of the vehicle
  • Company the vehicle was leased to
  • Color of the vehicle
  • Date of sale

Case 4: the following predictor variables might be useful, assuming that the relevant data are available:

  • Day of the week
  • Day of the year
  • Is the day before long weekend
  • Is the day in the end of long weekend
  • Is the day before or in the beginning of school holidays (one variable per every state)
  • Is the day in the end of school holidays (one variable per every state)
  • Is the day before or in the beginning of a major sport event
  • Is the day after of a major sport event
  • Competitors’ prices (relative to the price of the airline in question)
  • Is there a pilot strike at some of the competitors’ airlines
  • Is there a pilot strike at the airline in question

fpp3 1.8, Ex 2

For case 3 in Section 1.5, describe the five steps of forecasting in the context of this project.

1. Problem definition

  • The main stakeholders should be defined and everyone questioned about which way he or she can benefit from the new system. In case of the fleet company probably the group of specialists was not recognized as stakeholders which led to complications in gathering relevant information and later in finding an appropriate statistical approach and deployment of the new forecasting method.

2. Gathering information

  • Data set of past sales should be obtained, including surrounding information such as the way data were gathered, possible outliers and incorrect records, special values in the data.

  • Expertise knowledge should be obtained from people responsible for the sales such as seasonal price fluctuations, if there is dependency of the price on the situation in economy, also finding other possible factors which can influence the price.

3. Preliminary (exploratory) analysis

  • Possible outliers and inconsistent information should be found (for example very small, zero or even negative prices).

  • Graphs which show dependency of the sale price on different predictor variables should be considered.

  • Dependency of the sale price on month of the year should be plot.

4. Choosing and fitting models

  • A model to start from (for example a linear model) and predictor variables which most likely affect the forecasts should be chosen. Predicting performance of the model should be evaluated.

  • The model should be changed (for example by transforming parameters, adding or removing predictor variables) and it’s performance evaluated. This should be done iteratively a few times until a satisfactory model is found.

5. Using and evaluating a forecasting model

  • The appropriate software should be deployed to the company and relevant people should be educated how to use this software.

  • Forecasting accuracy should be checked against new sales. If necessary the model should be updated and then the deployed software.

fpp3 3.7, Ex 6

Show that a 3\times 5 MA is equivalent to a 7-term weighted moving average with weights of 0.067, 0.133, 0.200, 0.200, 0.200, 0.133, and 0.067.

5-term moving average: z_j = \frac{1}{5}(y_{j-2}+y_{j-1}+y_j+y_{j+1}+y_{j+2}). 3-term moving average: u_t = \frac{1}{3}(z_{t-1}+z_t+z_{t+1}). Substituting expression for z_j into the latter formula we get \begin{align*} u_t &= \frac{1}{3}\left(\frac{1}{5}\left(y_{t-3}+y_{t-2}+y_{t-1}+y_{t}+y_{t+1}\right)+\frac{1}{5}\left(y_{t-2}+y_{t-1}+y_t+y_{t+1}+y_{t+2}\right)+\frac{1}{5}\left(y_{t-1}+y_{t}+y_{t+1}+y_{t+2}+y_{t+3}\right)\right).\\ &= \frac{1}{15}\left(y_{t-3}+2y_{t-2}+3y_{t-1}+3y_{t}+3y_{t+1}+2y_{t+2}+y_{t+3}\right), \end{align*} which is a 7-term weighted moving average with weights of 0.067, 0.133, 0.200, 0.200, 0.200, 0.133, and 0.067

fpp3 3.7, Ex 7

Consider the last five years of the Gas data from aus_production.

gas <- tail(aus_production, 5*4) |> select(Gas)
  1. Plot the time series. Can you identify seasonal fluctuations and/or a trend-cycle?
gas <- tail(aus_production, 5 * 4) |> select(Gas)
gas |>
  autoplot(Gas) + labs(y = "Petajoules")

There is some strong seasonality and a trend.

  1. Use classical_decomposition with type=multiplicative to calculate the trend-cycle and seasonal indices.
  2. Do the results support the graphical interpretation from part a?
decomp <- gas |>
  model(decomp = classical_decomposition(Gas, type = "multiplicative")) |>
  components()
decomp |> autoplot()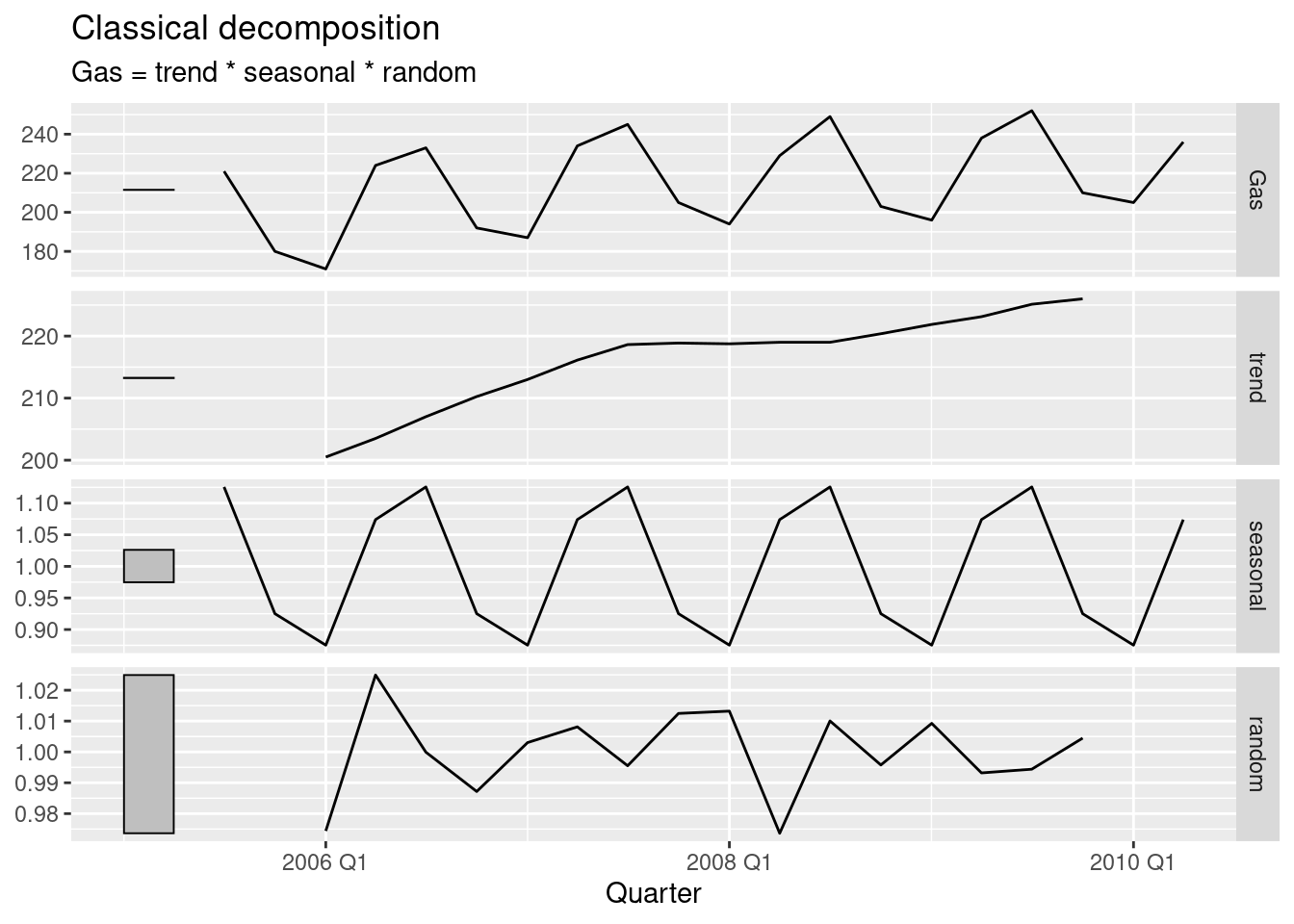

The decomposition has captured the seasonality and a slight trend.

  1. Compute and plot the seasonally adjusted data.
as_tsibble(decomp) |>
  autoplot(season_adjust) +
  labs(title = "Seasonally adjusted data", y = "Petajoules")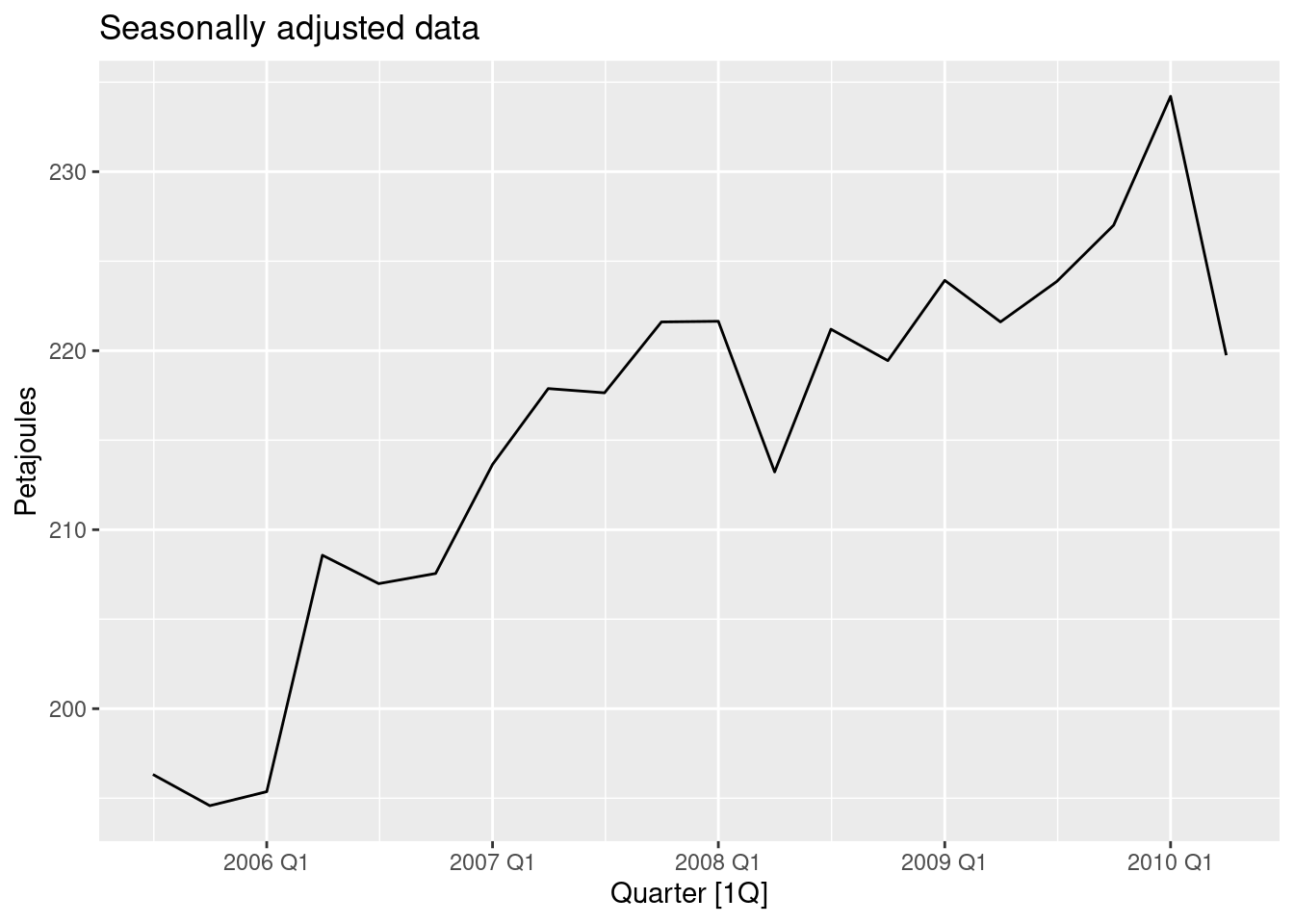

  1. Change one observation to be an outlier (e.g., add 300 to one observation), and recompute the seasonally adjusted data. What is the effect of the outlier?
  2. Does it make any difference if the outlier is near the end rather than in the middle of the time series?
gas |>
  mutate(Gas = if_else(Quarter == yearquarter("2007Q4"), Gas + 300, Gas)) |>
  model(decomp = classical_decomposition(Gas, type = "multiplicative")) |>
  components() |>
  as_tsibble() |>
  autoplot(season_adjust) +
  labs(title = "Seasonally adjusted data", y = "Petajoules")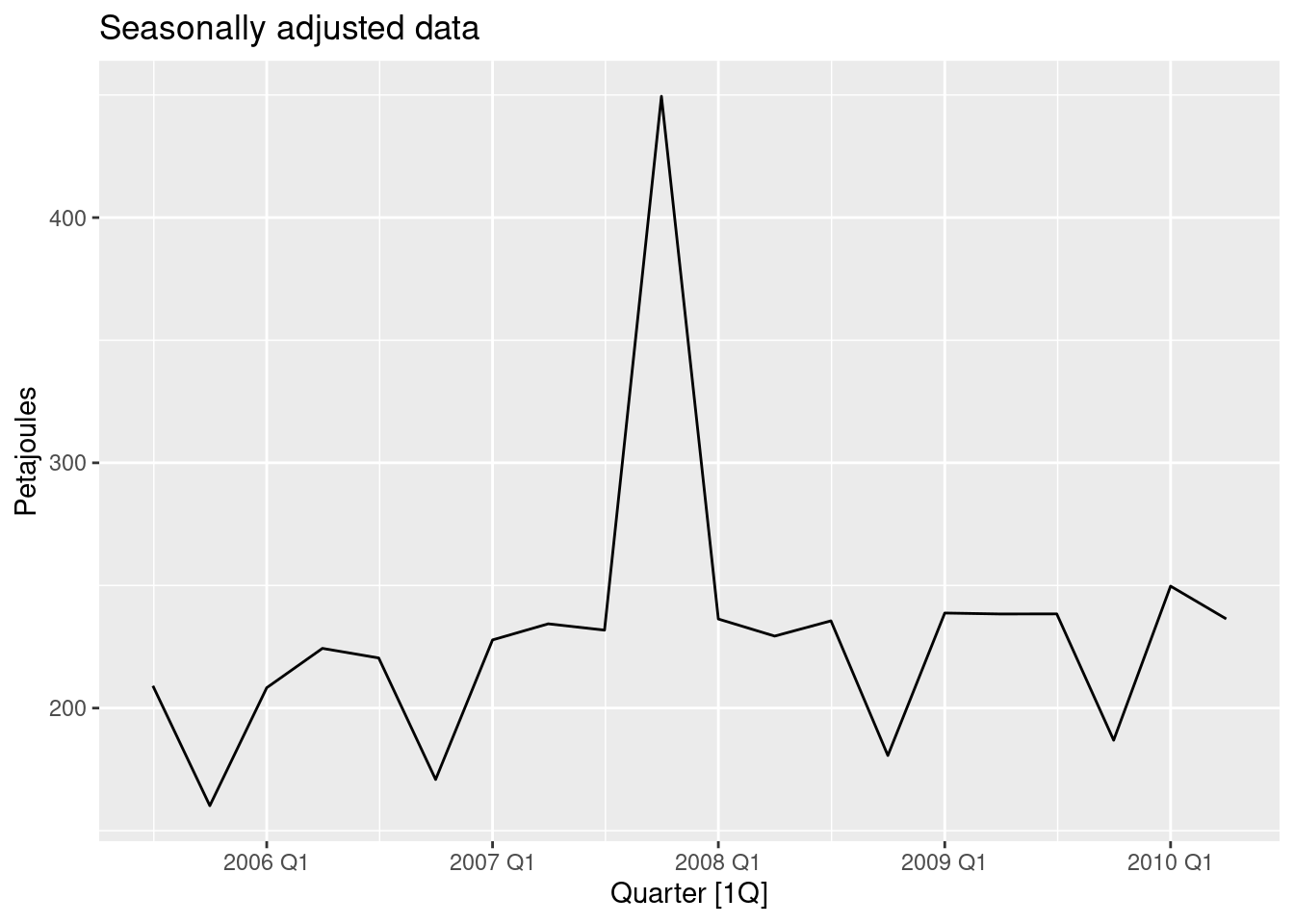

  • The “seasonally adjusted” data now shows some seasonality because the outlier has affected the estimate of the seasonal component.
gas |>
  mutate(Gas = if_else(Quarter == yearquarter("2010Q2"), Gas + 300, Gas)) |>
  model(decomp = classical_decomposition(Gas, type = "multiplicative")) |>
  components() |>
  as_tsibble() |>
  autoplot(season_adjust) +
  labs(title = "Seasonally adjusted data", y = "Petajoules")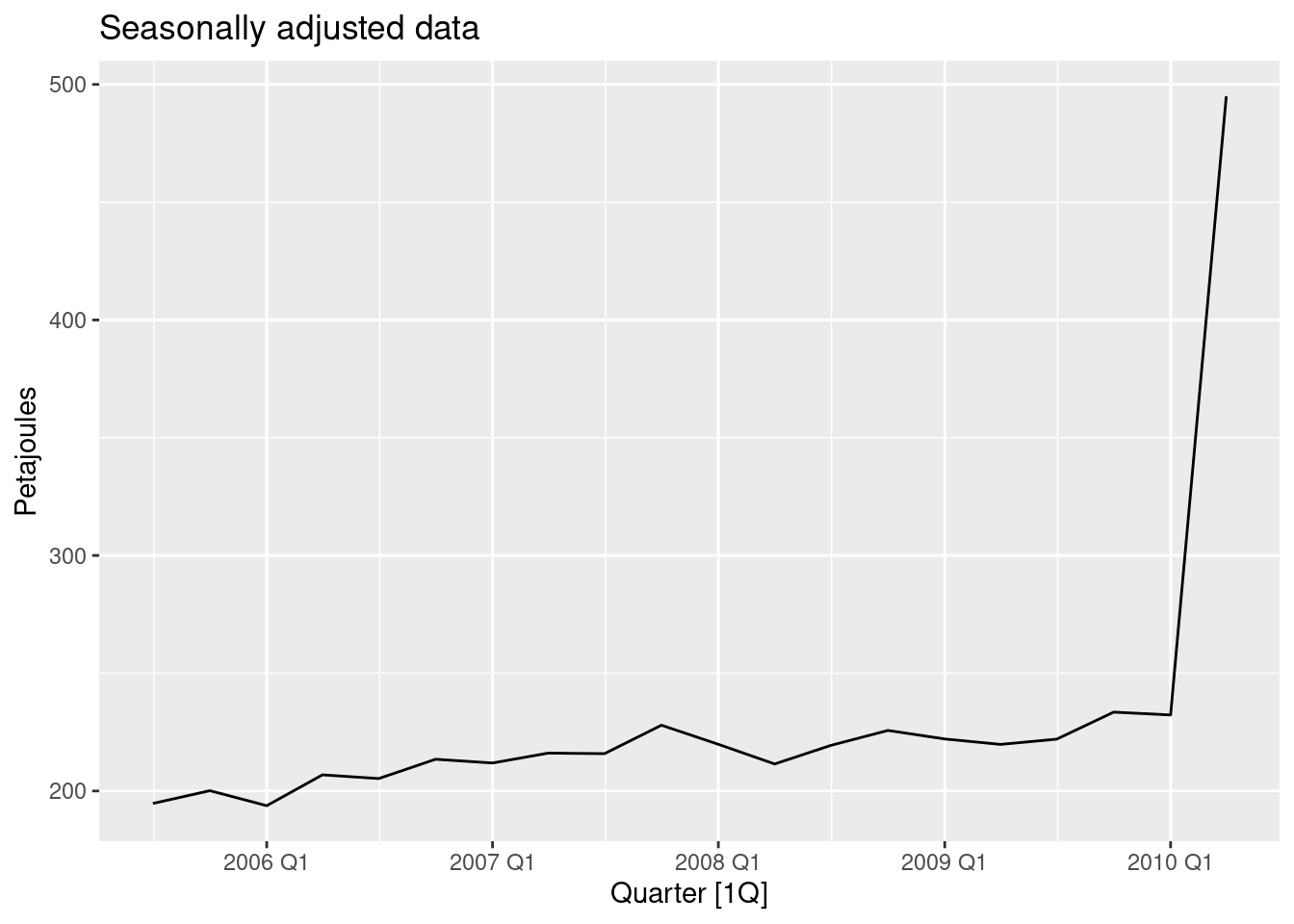

The seasonally adjusted data now show no seasonality because the outlier is in the part of the data where the trend can’t be estimated.

fpp3 3.7, Ex 8

Recall your retail time series data (from Exercise 8 in Section 2.10). Decompose the series using X11. Does it reveal any outliers, or unusual features that you had not noticed previously?

set.seed(12345678)
myseries <- aus_retail |>
  filter(`Series ID` == sample(aus_retail$`Series ID`, 1))
decomp <- myseries |>
  model(x11 = X_13ARIMA_SEATS(Turnover ~ x11())) |>
  components()
decomp |> autoplot()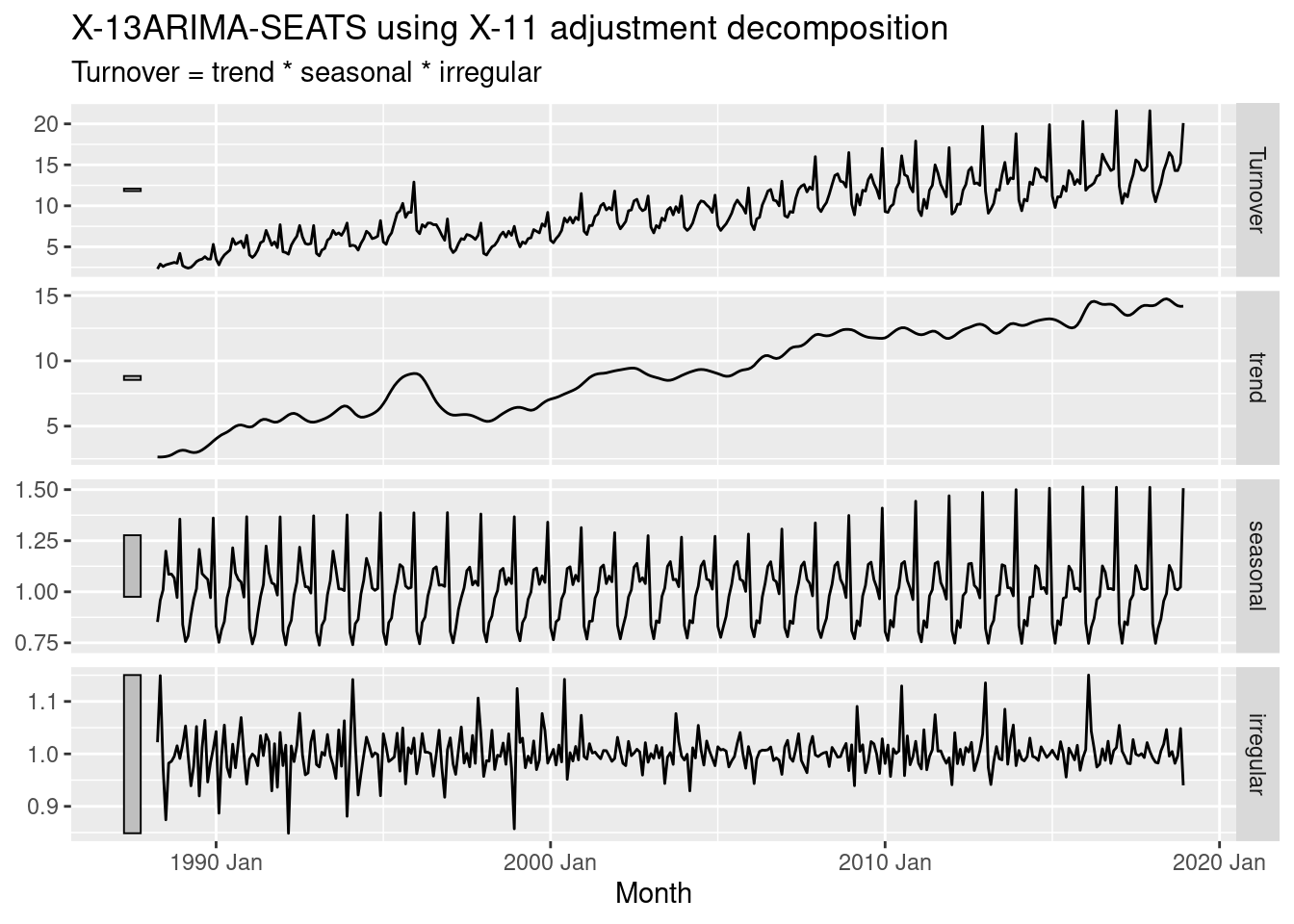

Two outliers are now evident in the “irregular” component — in December 1995 and July 2010.

fpp3 5.10, Ex 7

For your retail time series (from Exercise 8 in Section 2.10):

  1. Create a training dataset consisting of observations before 2011.
  2. Check that your data have been split appropriately by producing the following plot.
  3. Calculate seasonal naïve forecasts using SNAIVE() applied to your training data (myseries_train).
  4. Check the residuals. Do the residuals appear to be uncorrelated and normally distributed?
  5. Produce forecasts for the test data.
  6. Compare the accuracy of your forecasts against the actual values.
  7. How sensitive are the accuracy measures to the amount of training data used?
set.seed(12345678)
myseries <- aus_retail |>
  filter(`Series ID` == sample(aus_retail$`Series ID`, 1))
myseries_train <- myseries |>
  filter(year(Month) < 2011)
autoplot(myseries, Turnover) +
  autolayer(myseries_train, Turnover, colour = "red")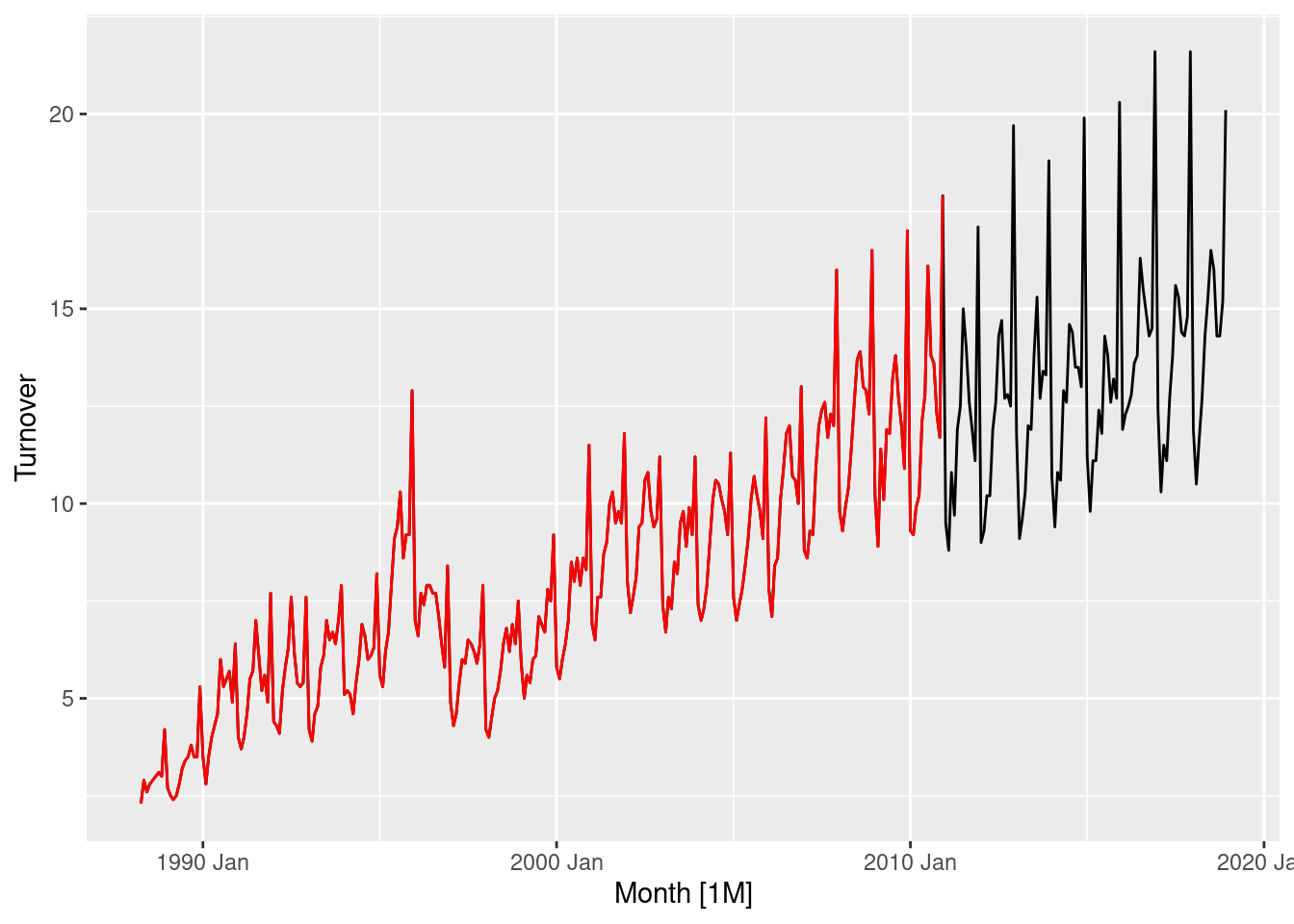

The plot indicates that the training data has been extracted correctly.

fit <- myseries_train |>
  model(SNAIVE(Turnover))
fit |> gg_tsresiduals()

The residuals appear very auto-correlated as many lags exceed the significance threshold. This can also be seen in the residual plot, where there are periods of sustained high and low residuals. The distribution does not appear normally distributed, and is not centred around zero.

fc <- fit |>
  forecast(new_data = anti_join(myseries, myseries_train))
fc |> autoplot(myseries)

bind_rows(
  accuracy(fit),
  accuracy(fc, myseries)
) |>
  select(-State, -Industry, -.model)
# A tibble: 2 × 9
  .type       ME  RMSE   MAE   MPE  MAPE  MASE RMSSE  ACF1
  <chr>    <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Training 0.439  1.21 0.915  5.23 12.4   1     1    0.768
2 Test     0.836  1.55 1.24   5.94  9.06  1.36  1.28 0.601

The accuracy on the training data is substantially better than the out-of-sample forecast accuracy. This is common, and especially evident in this example as the model has failed to capture the trend in the data. This can be seen in the mean error, which is above zero as the model predictions do not account for the upward trend.

myseries_accuracy <- function(data, last_training_year) {
  myseries_train <- data |>
    filter(year(Month) <= last_training_year)
  fit <- myseries_train |>
    model(SNAIVE(Turnover))
  fc <- fit |>
    forecast(new_data = anti_join(myseries, myseries_train))
  bind_rows(
    accuracy(fit),
    accuracy(fc, myseries)
  ) |>
    mutate(last_training_year = last_training_year) |>
    select(last_training_year, .type, ME:ACF1)
}
as.list(2011:2017) |>
  purrr::map_dfr(myseries_accuracy, data = myseries) |>
  ggplot(aes(x = last_training_year, y = RMSE, group = .type)) +
  geom_line(aes(col = .type))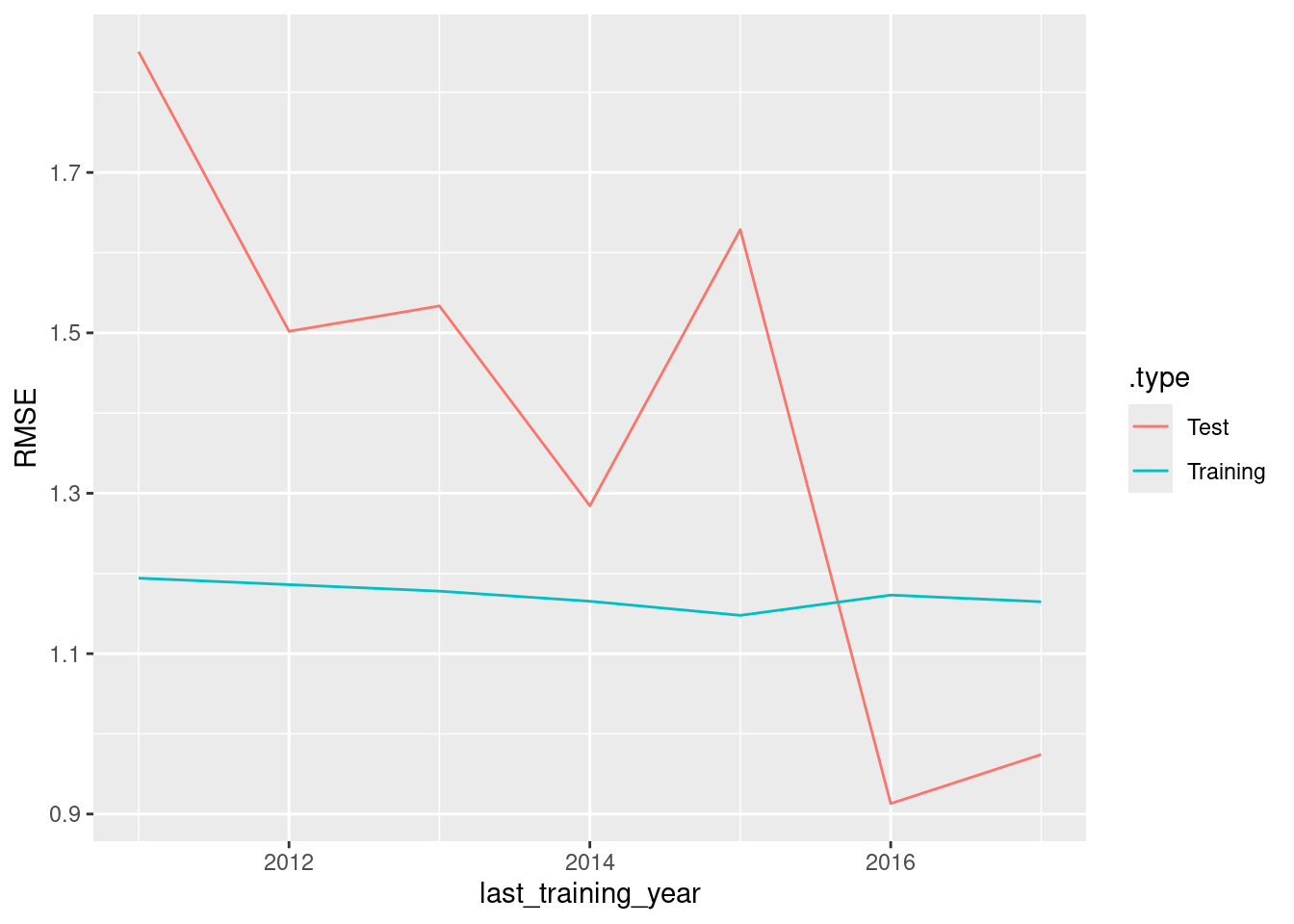

The accuracy on the training data is almost unchanged when the size of the training set is increased. However, the accuracy on the test data decreases as we are averaging RMSE over the forecast horizon, and with less training data the forecasts horizons can be longer.

fpp3 5.10, Ex 9

  1. Create a training set for household wealth (hh_budget) by withholding the last four years as a test set.
train <- hh_budget |>
  filter(Year <= max(Year) - 4)
  1. Fit all the appropriate benchmark methods to the training set and forecast the periods covered by the test set.
fit <- train |>
  model(
    naive = NAIVE(Wealth),
    drift = RW(Wealth ~ drift()),
    mean = MEAN(Wealth)
  )
fc <- fit |> forecast(h = 4)
  1. Compute the accuracy of your forecasts. Which method does best?
fc |>
  accuracy(hh_budget) |>
  arrange(Country, MASE)
# A tibble: 12 × 11
   .model Country   .type    ME  RMSE   MAE   MPE  MAPE  MASE RMSSE    ACF1
   <chr>  <chr>     <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>   <dbl>
 1 drift  Australia Test   29.1  35.5  29.1  7.23  7.23 1.73  1.48   0.210 
 2 naive  Australia Test   34.7  41.5  34.7  8.64  8.64 2.06  1.73   0.216 
 3 mean   Australia Test   35.7  42.3  35.7  8.89  8.89 2.12  1.76   0.216 
 4 drift  Canada    Test   33.3  37.2  33.3  6.09  6.09 1.73  1.57  -0.229 
 5 naive  Canada    Test   46.2  51.0  46.2  8.46  8.46 2.40  2.15  -0.0799
 6 mean   Canada    Test   90.4  92.9  90.4 16.7  16.7  4.69  3.92  -0.0799
 7 drift  Japan     Test   14.7  17.9  14.7  2.44  2.44 0.943 0.967 -0.229 
 8 naive  Japan     Test   36.3  37.8  36.3  6.06  6.06 2.34  2.04  -0.534 
 9 mean   Japan     Test  100.  101.  100.  16.8  16.8  6.45  5.46  -0.534 
10 drift  USA       Test   75.9  76.2  75.9 12.7  12.7  2.88  2.43  -0.561 
11 naive  USA       Test   82.1  82.5  82.1 13.8  13.8  3.12  2.63  -0.423 
12 mean   USA       Test   82.9  83.3  82.9 13.9  13.9  3.15  2.65  -0.423 
fc |>
  accuracy(hh_budget) |>
  group_by(.model) |>
  summarise(MASE = mean(MASE)) |>
  ungroup() |>
  arrange(MASE)
# A tibble: 3 × 2
  .model  MASE
  <chr>  <dbl>
1 drift   1.82
2 naive   2.48
3 mean    4.10

The drift method is better for every country, and on average.

  1. Do the residuals from the best method resemble white noise?
fit |>
  filter(Country == "Australia") |>
  select(drift) |>
  gg_tsresiduals()

fit |>
  filter(Country == "Canada") |>
  select(drift) |>
  gg_tsresiduals()

fit |>
  filter(Country == "Japan") |>
  select(drift) |>
  gg_tsresiduals()

fit |>
  filter(Country == "USA") |>
  select(drift) |>
  gg_tsresiduals()

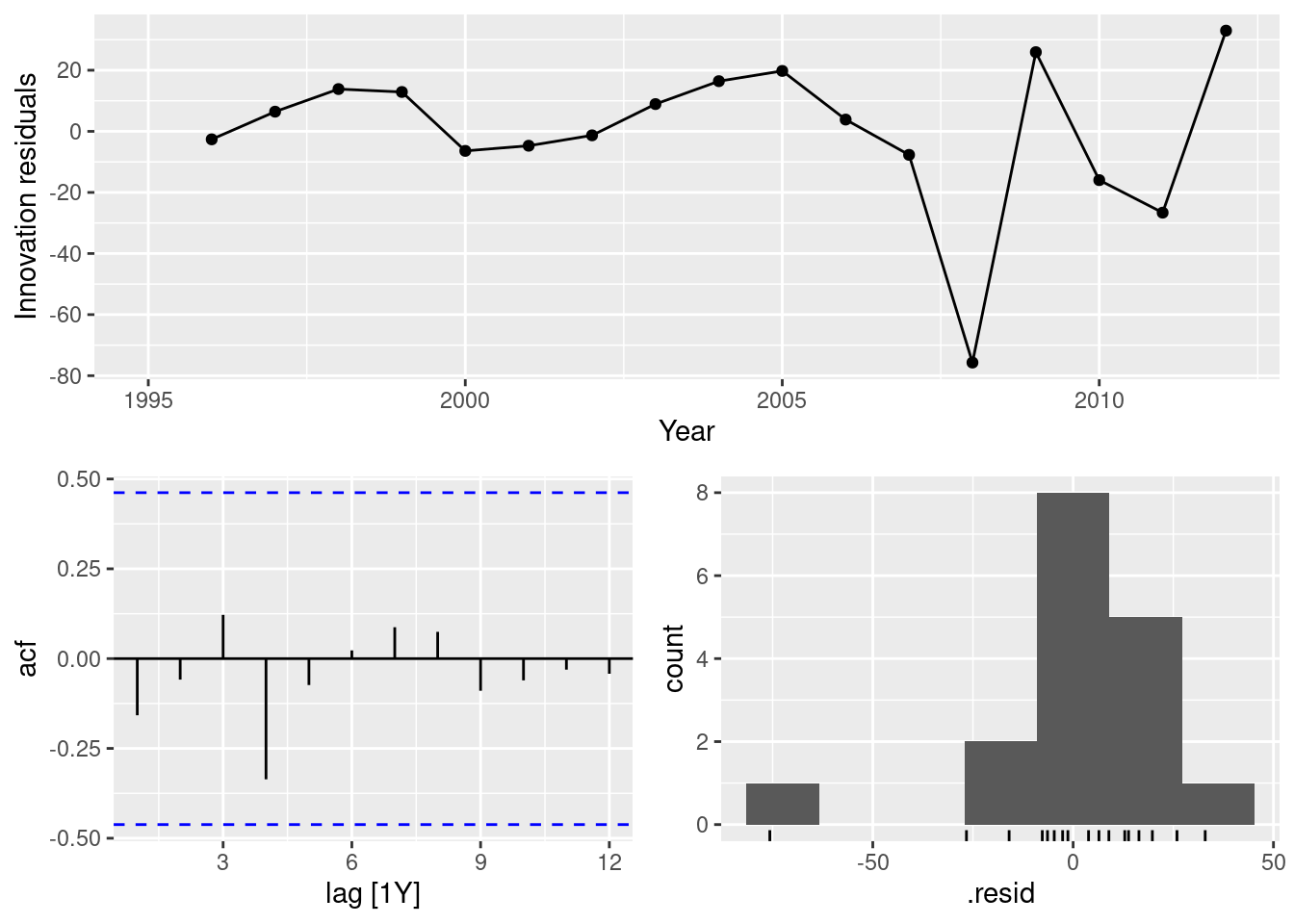
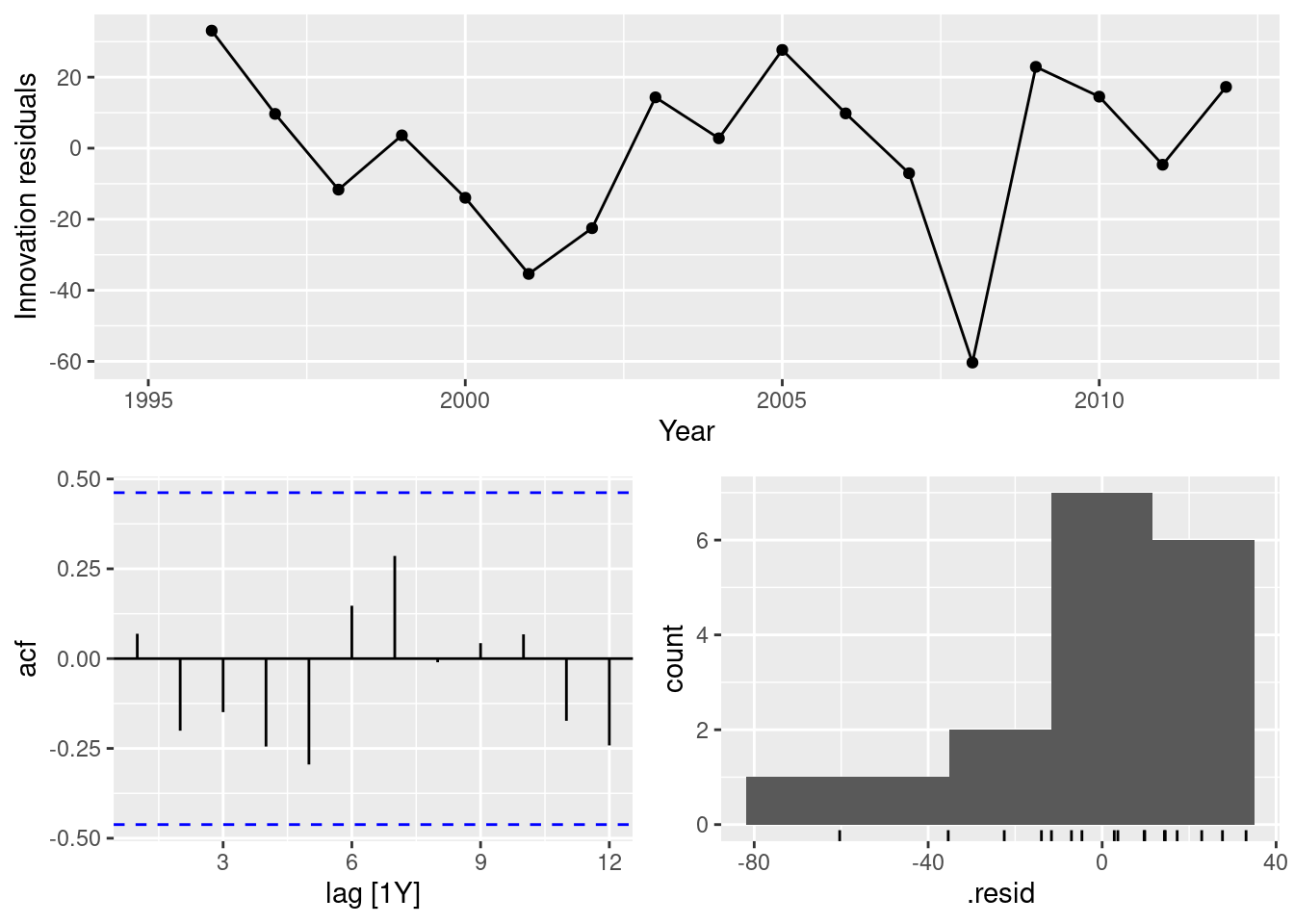
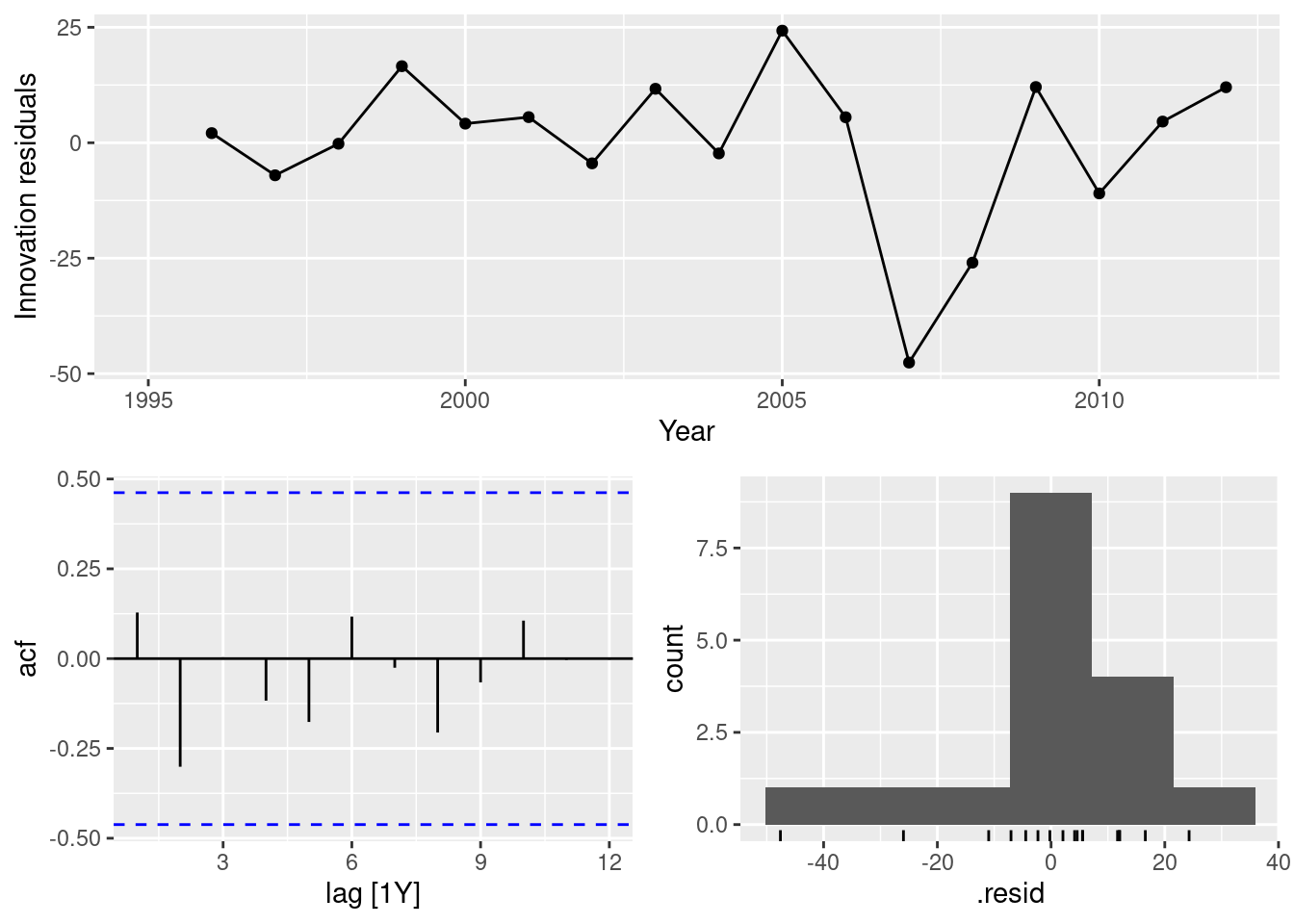
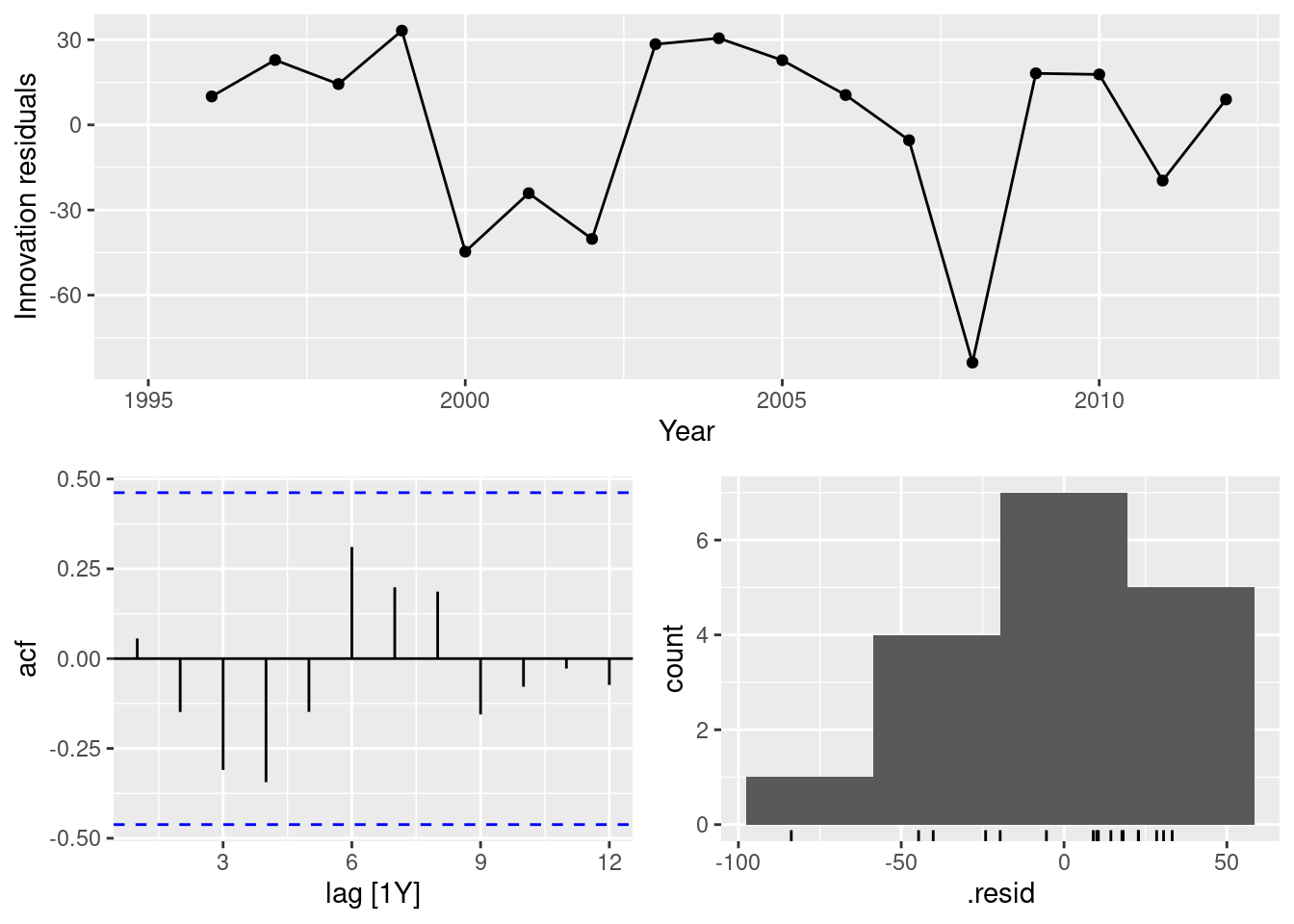
In all cases, the residuals look like white noise.

fpp3 5.10, Ex 10

  1. Create a training set for Australian takeaway food turnover (aus_retail) by withholding the last four years as a test set.
takeaway <- aus_retail |>
  filter(Industry == "Takeaway food services") |>
  summarise(Turnover = sum(Turnover))
train <- takeaway |>
  filter(Month <= max(Month) - 4 * 12)
  1. Fit all the appropriate benchmark methods to the training set and forecast the periods covered by the test set.
fit <- train |>
  model(
    naive = NAIVE(Turnover),
    drift = RW(Turnover ~ drift()),
    mean = MEAN(Turnover),
    snaive = SNAIVE(Turnover)
  )
fc <- fit |> forecast(h = "4 years")
  1. Compute the accuracy of your forecasts. Which method does best?
fc |>
  accuracy(takeaway) |>
  arrange(MASE)
# A tibble: 4 × 10
  .model .type    ME  RMSE   MAE   MPE  MAPE  MASE RMSSE  ACF1
  <chr>  <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 naive  Test  -12.4  119.  96.4 -1.49  6.66  2.30  2.25 0.613
2 drift  Test  -93.7  130. 108.  -6.82  7.67  2.58  2.46 0.403
3 snaive Test  177.   192. 177.  11.7  11.7   4.22  3.64 0.902
4 mean   Test  829.   838. 829.  55.7  55.7  19.8  15.8  0.613

The naive method is best here.

  1. Do the residuals from the best method resemble white noise?
fit |>
  select(naive) |>
  gg_tsresiduals()

This is far from white noise. There is strong seasonality and increasing variance that has not been accounted for by the naive model.

fpp3 8.8, Ex6

Forecast the Chinese GDP from the global_economy data set using an ETS model. Experiment with the various options in the ETS() function to see how much the forecasts change with damped trend, or with a Box-Cox transformation. Try to develop an intuition of what each is doing to the forecasts.

[Hint: use h=20 when forecasting, so you can clearly see the differences between the various options when plotting the forecasts.]

china <- global_economy |>
  filter(Country == "China")
china |> autoplot(GDP)

  • It clearly needs a relatively strong transformation due to the increasing variance.
china |> autoplot(box_cox(GDP, 0.2))

china |> features(GDP, guerrero)
# A tibble: 1 × 2
  Country lambda_guerrero
  <fct>             <dbl>
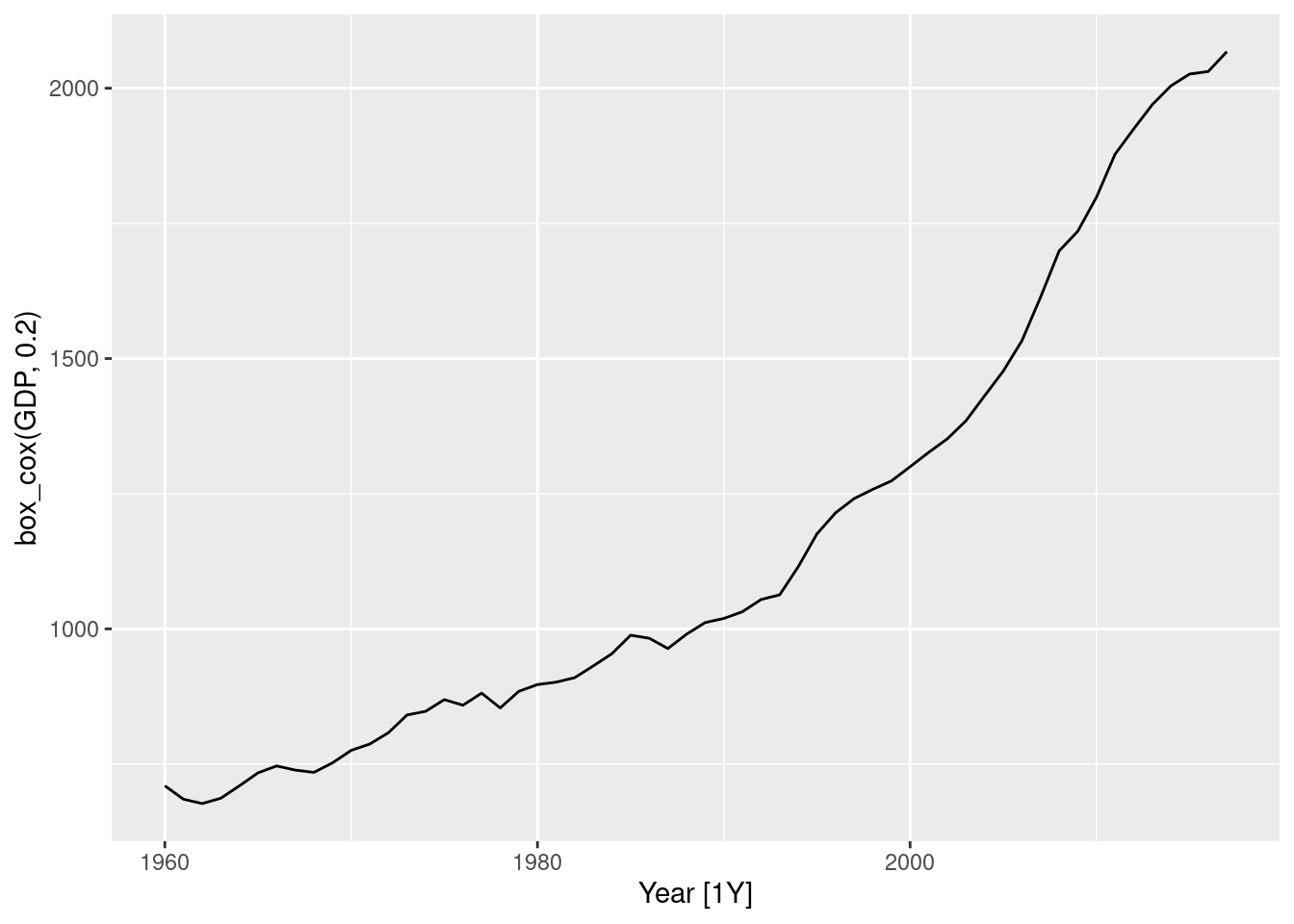
1 China           -0.0345

  • Making \lambda=0.2 looks ok.

  • The Guerrero method suggests an even stronger transformation. Let’s also try a log.

fit <- china |>
  model(
    ets = ETS(GDP),
    ets_damped = ETS(GDP ~ trend("Ad")),
    ets_bc = ETS(box_cox(GDP, 0.2)),
    ets_log = ETS(log(GDP))
  )

fit
# A mable: 1 x 5
# Key:     Country [1]
  Country          ets    ets_damped       ets_bc      ets_log
  <fct>        <model>       <model>      <model>      <model>
1 China   <ETS(M,A,N)> <ETS(M,Ad,N)> <ETS(A,A,N)> <ETS(A,A,N)>
augment(fit)
# A tsibble: 232 x 7 [1Y]
# Key:       Country, .model [4]
   Country .model  Year          GDP      .fitted        .resid   .innov
   <fct>   <chr>  <dbl>        <dbl>        <dbl>         <dbl>    <dbl>
 1 China   ets     1960 59716467625. 49001691297.  10714776328.  0.219  
 2 China   ets     1961 50056868958. 66346643194. -16289774236. -0.246  
 3 China   ets     1962 47209359006. 51607368186.  -4398009180. -0.0852 
 4 China   ets     1963 50706799903. 47386494407.   3320305495.  0.0701 
 5 China   ets     1964 59708343489. 51919091574.   7789251914.  0.150  
 6 China   ets     1965 70436266147. 63350421234.   7085844913.  0.112  
 7 China   ets     1966 76720285970. 76289186599.    431099371.  0.00565
 8 China   ets     1967 72881631327. 82708375812.  -9826744486. -0.119  
 9 China   ets     1968 70846535056. 75804820984.  -4958285928. -0.0654 
10 China   ets     1969 79705906247. 72222259470.   7483646777.  0.104  
# ℹ 222 more rows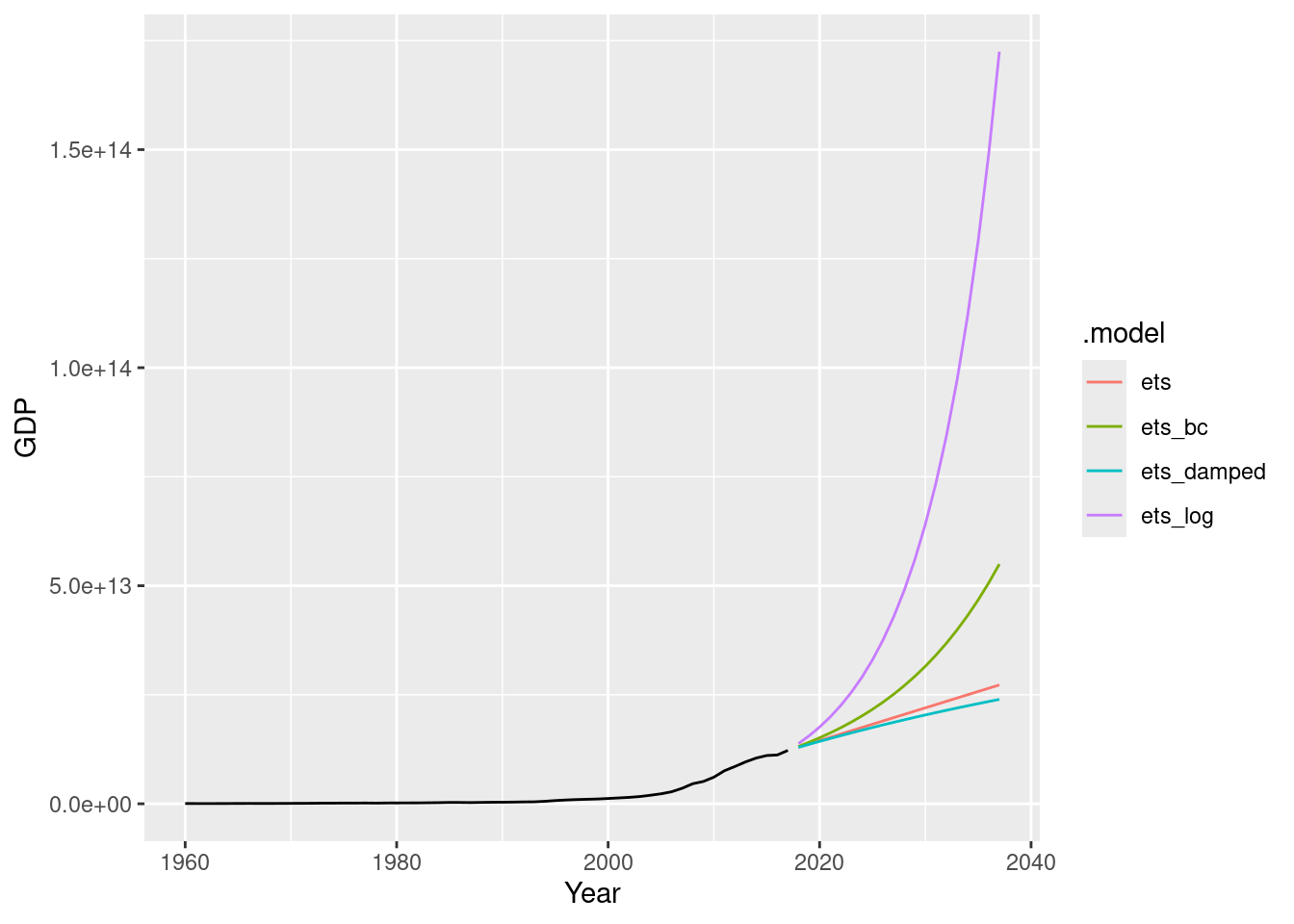
fit |>
  forecast(h = "20 years") |>
  autoplot(china, level = NULL)

  • The transformations have a big effect, with small lambda values creating big increases in the forecasts.
  • The damping has relatively a small effect.

fpp3 8.8, Ex7

Find an ETS model for the Gas data from aus_production and forecast the next few years. Why is multiplicative seasonality necessary here? Experiment with making the trend damped. Does it improve the forecasts?

aus_production |> autoplot(Gas)

  • There is a huge increase in variance as the series increases in level. => That makes it necessary to use multiplicative seasonality.
fit <- aus_production |>
  model(
    hw = ETS(Gas ~ error("M") + trend("A") + season("M")),
    hwdamped = ETS(Gas ~ error("M") + trend("Ad") + season("M")),
  )

fit |> glance()
# A tibble: 2 × 9
  .model    sigma2 log_lik   AIC  AICc   BIC   MSE  AMSE    MAE
  <chr>      <dbl>   <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl>
1 hw       0.00324   -831. 1681. 1682. 1711.  21.1  32.2 0.0413
2 hwdamped 0.00329   -832. 1684. 1685. 1718.  21.1  32.0 0.0417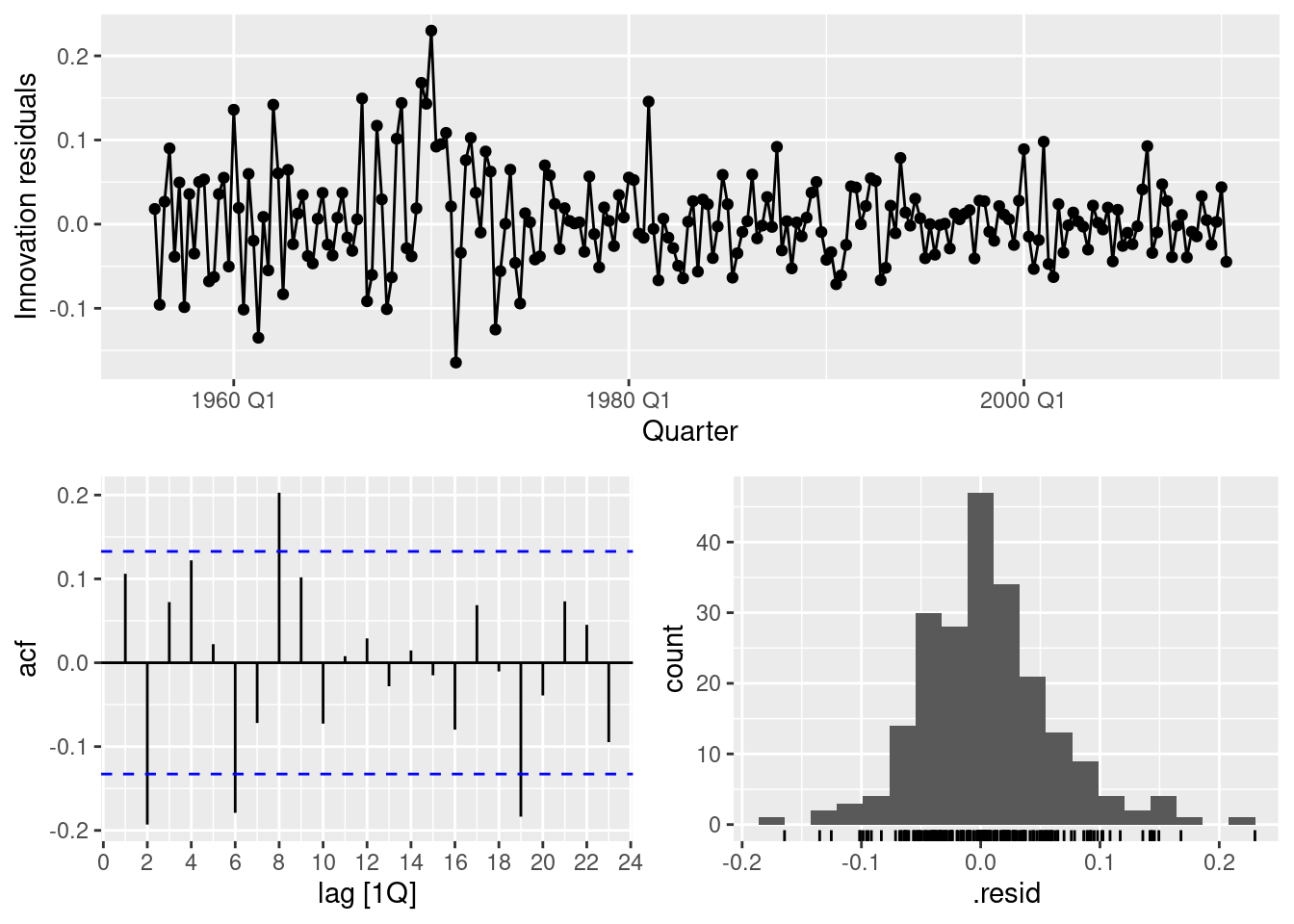
  • The non-damped model seems to be doing slightly better here, probably because the trend is very strong over most of the historical data.
fit |>
  select(hw) |>
  gg_tsresiduals()

fit |> tidy()
# A tibble: 19 × 3
   .model   term  estimate
   <chr>    <chr>    <dbl>
 1 hw       alpha   0.653 
 2 hw       beta    0.144 
 3 hw       gamma   0.0978
 4 hw       l[0]    5.95  
 5 hw       b[0]    0.0706
 6 hw       s[0]    0.931 
 7 hw       s[-1]   1.18  
 8 hw       s[-2]   1.07  
 9 hw       s[-3]   0.816 
10 hwdamped alpha   0.649 
11 hwdamped beta    0.155 
12 hwdamped gamma   0.0937
13 hwdamped phi     0.980 
14 hwdamped l[0]    5.86  
15 hwdamped b[0]    0.0994
16 hwdamped s[0]    0.928 
17 hwdamped s[-1]   1.18  
18 hwdamped s[-2]   1.08  
19 hwdamped s[-3]   0.817 
fit |>
  augment() |>
  filter(.model == "hw") |>
  features(.innov, ljung_box, lag = 24)
# A tibble: 1 × 3
  .model lb_stat lb_pvalue
  <chr>    <dbl>     <dbl>
1 hw        57.1  0.000161
  • There is still some small correlations left in the residuals, showing the model has not fully captured the available information.
  • There also appears to be some heteroskedasticity in the residuals with larger variance in the first half the series.
fit |>
  forecast(h = 36) |>
  filter(.model == "hw") |>
  autoplot(aus_production)

While the point forecasts look ok, the intervals are excessively wide.

fpp3 10.7, Ex 1

This exercise uses data set LakeHuron giving the level of Lake Huron from 1875–1972.

  1. Convert the data to a tsibble object using the as_tsibble() function.
  2. Fit a piecewise linear trend model to the Lake Huron data with a knot at 1920 and an ARMA error structure.
  3. Forecast the level for the next 30 years. Do you think the extrapolated linear trend is realistic?
huron <- as_tsibble(LakeHuron)
fit <- huron |>
  model(ARIMA(value ~ trend(knot = 1920)))
report(fit)
Series: value 
Model: LM w/ ARIMA(2,0,0) errors 

Coefficients:
         ar1      ar2  trend(knot = 1920)trend  trend(knot = 1920)trend_46
      0.9628  -0.3107                  -0.0572                      0.0633
s.e.  0.0973   0.0983                   0.0161                      0.0265
      intercept
       580.9391
s.e.     0.5124

sigma^2 estimated as 0.4594:  log likelihood=-98.86
AIC=209.73   AICc=210.65   BIC=225.24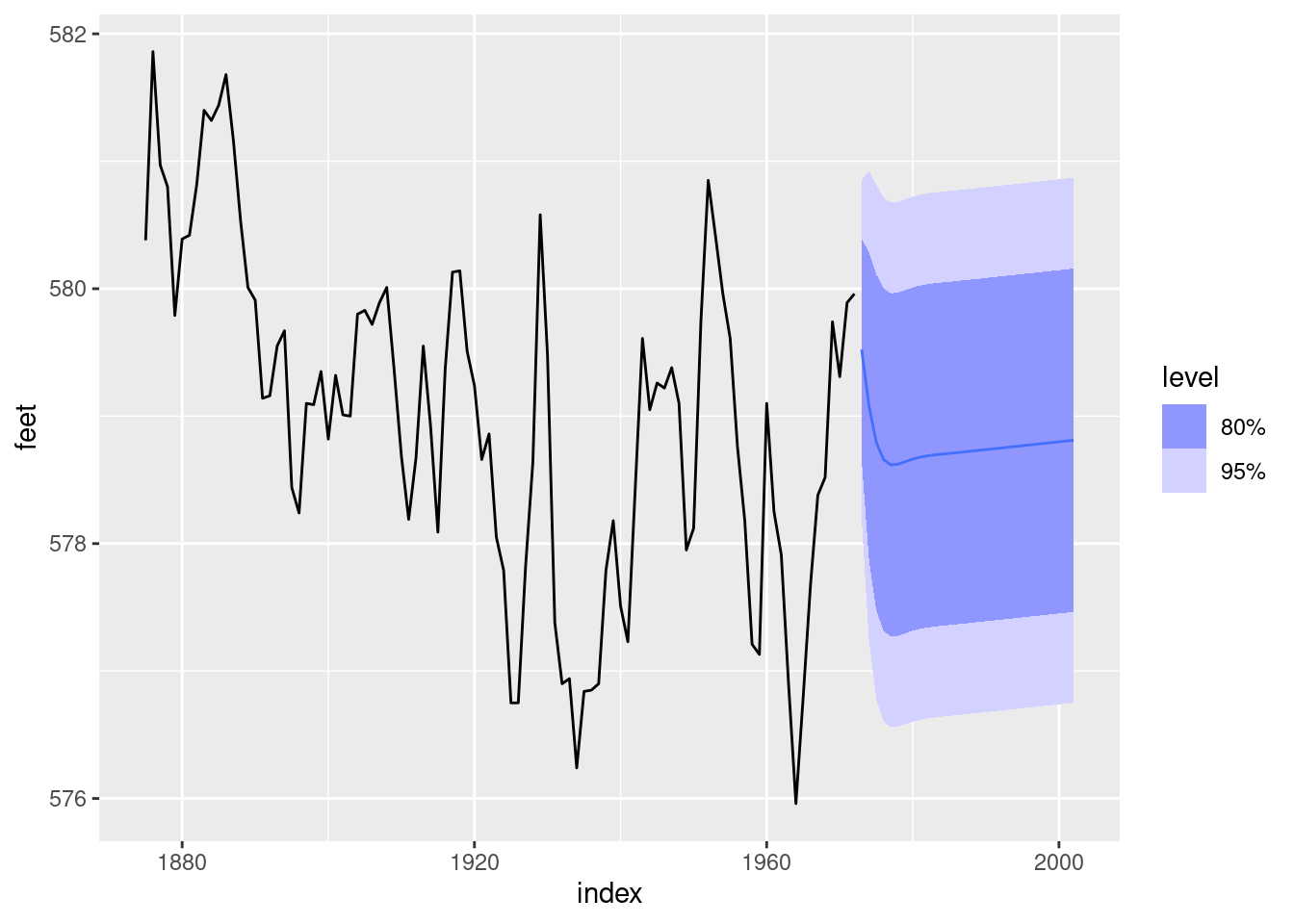
fit |>
  forecast(h = 30) |>
  autoplot(huron) + labs(y = "feet")

It seems unlikely that there was an increasing trend from 1973 to 2002, but the prediction intervals are very wide so they probably capture the actual values. Historical data on the level of Lake Huron can be obtained from the NOAA.

fpp3 10.7, Ex 7

For the retail time series considered in earlier chapters:

  1. Develop an appropriate dynamic regression model with Fourier terms for the seasonality. Use the AIC to select the number of Fourier terms to include in the model. (You will probably need to use the same Box-Cox transformation you identified previously.)
set.seed(12345678)
myseries <- aus_retail |>
  filter(
    `Series ID` == sample(aus_retail$`Series ID`, 1),
    Month < yearmonth("2018 Jan")
  )

myseries |> features(Turnover, guerrero)
# A tibble: 1 × 3
  State              Industry                                    lambda_guerrero
  <chr>              <chr>                                                 <dbl>
1 Northern Territory Clothing, footwear and personal accessory …          0.0776
myseries |> autoplot(log(Turnover))

fit <- myseries |>
  model(
    `K=1` = ARIMA(log(Turnover) ~ trend() + fourier(K = 1) +
      pdq(0:2, 0, 0:2) + PDQ(0:1, 0, 0:1)),
    `K=2` = ARIMA(log(Turnover) ~ trend() + fourier(K = 2) +
      pdq(0:2, 0, 0:2) + PDQ(0:1, 0, 0:1)),
    `K=3` = ARIMA(log(Turnover) ~ trend() + fourier(K = 3) +
      pdq(0:2, 0, 0:2) + PDQ(0:1, 0, 0:1)),
    `K=4` = ARIMA(log(Turnover) ~ trend() + fourier(K = 4) +
      pdq(0:2, 0, 0:2) + PDQ(0:1, 0, 0:1)),
    `K=5` = ARIMA(log(Turnover) ~ trend() + fourier(K = 5) +
      pdq(0:2, 0, 0:2) + PDQ(0:1, 0, 0:1)),
    `K=6` = ARIMA(log(Turnover) ~ trend() + fourier(K = 6) +
      pdq(0:2, 0, 0:2) + PDQ(0:1, 0, 0:1))
  )
glance(fit)
# A tibble: 6 × 10
  State      Industry .model  sigma2 log_lik   AIC  AICc   BIC ar_roots ma_roots
  <chr>      <chr>    <chr>    <dbl>   <dbl> <dbl> <dbl> <dbl> <list>   <list>  
1 Northern … Clothin… K=1    0.00664    383. -748. -748. -713. <cpl>    <cpl>   
2 Northern … Clothin… K=2    0.00652    389. -756. -755. -713. <cpl>    <cpl>   
3 Northern … Clothin… K=3    0.00626    400. -774. -773. -723. <cpl>    <cpl>   
4 Northern … Clothin… K=4    0.00596    411. -792. -791. -734. <cpl>    <cpl>   
5 Northern … Clothin… K=5    0.00480    453. -873. -872. -811. <cpl>    <cpl>   
6 Northern … Clothin… K=6    0.00437    470. -906. -905. -841. <cpl>    <cpl>

Including 6 harmonics minimises the AICc (and AIC/BIC) for this series.

fit <- transmute(fit, best = `K=6`)

report(fit)
Series: Turnover 
Model: LM w/ ARIMA(1,0,1)(1,0,0)[12] errors 
Transformation: log(Turnover) 

Coefficients:
         ar1      ma1    sar1  trend()  fourier(K = 6)C1_12
      0.9632  -0.3755  0.1761   0.0041              -0.0809
s.e.  0.0165   0.0502  0.0542   0.0006               0.0080
      fourier(K = 6)S1_12  fourier(K = 6)C2_12  fourier(K = 6)S2_12
                  -0.1258               0.0381              -0.0882
s.e.               0.0080               0.0052               0.0052
      fourier(K = 6)C3_12  fourier(K = 6)S3_12  fourier(K = 6)C4_12
                  -0.0206              -0.0815              -0.0294
s.e.               0.0045               0.0045               0.0042
      fourier(K = 6)S4_12  fourier(K = 6)C5_12  fourier(K = 6)S5_12
                  -0.0538              -0.0554              -0.0540
s.e.               0.0042               0.0041               0.0041
      fourier(K = 6)C6_12  intercept
                  -0.0230     1.3317
s.e.               0.0029     0.1231

sigma^2 estimated as 0.004368:  log likelihood=470.23
AIC=-906.46   AICc=-904.65   BIC=-840.54

The chosen model is a linear trend (will be exponential after back-transforming) and fourier terms with 5 harmonics. The error model is ARIMA(1,0,1)(1,0,1).

  1. Check the residuals of the fitted model. Does the residual series look like white noise?
gg_tsresiduals(fit)

The residuals look well behaved.

  1. Compare the forecasts with those you obtained earlier using alternative models.
fit <- myseries |>
  model(
    dynamic = ARIMA(log(Turnover) ~ trend() + fourier(K = 6) +
      pdq(0:2, 0, 0:2) + PDQ(0:1, 0, 0:1)),
    arima = ARIMA(log(Turnover)),
    ets = ETS(Turnover)
  )
fit |>
  forecast() |>
  autoplot(filter(myseries, year(Month) > 2010), level = 80, alpha = 0.5)